Sudoku

Este término de origen japonés (Su: número, Doku: único) define un juego mental muy popular de pensamiento lógico, razonamiento y paciencia. Existen Sudokus de todos los niveles, de forma que es un juego apto para todos los públicos. Cada uno tiene una única forma de resolverse. La cantidad de combinaciones posibles es limitada pero muy alta, se estima que podría haber más de 5000 millones de combinaciones posibles.

Las reglas del juego son muy sencillas. El Sudoku está formado por una cuadrícula de 9x9 casillas. Se trata de rellenar las celdas con números del 1 al 9 de forma que no se repita ningún número en cada fila y en cada columna. Además, el tablero se divide en 9 regiones de 3x3 celdas, de forma que en cada región tampoco se puede repetir ningún número. Algunas casillas están rellenas de forma predeterminada desde el principio, lo cual condicionará la dificultad del juego.

En la siguiente imagen vemos un ejemplo de una partida de Sudoku y su respuesta:

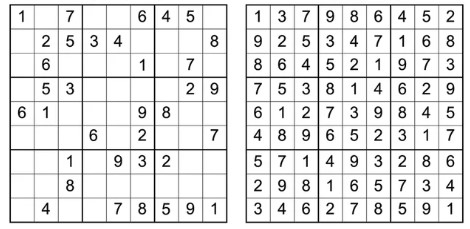
Desde el punto de vista de su resolución, los algoritmos de vuelta atrás son adecuados para resolver los sudokus. Recordemos que estos algoritmos recorren una estructura de árbol para encontrar los nodos que cumplan con determinados requisitos. Si adaptamos esta idea al Sudoku, cada nodo representaría una combinación posible de números en el tablero que cuando se complete podría ser una solución. A la hora de recorrer el árbol de soluciones, sólo continuaremos la exploración por un nodo si comprobamos que es una solución k-prometedora, es decir, si a partir de esta solución parcial podemos seguir construyendo soluciones parciales. Para ello, haremos uso de la función esFactible, que comprobará que no se rompen las reglas del Sudoku, es decir, que no se repite un número en la fila, columna y región de 3x3 celdas.

En la página de visualización podrás ver el código del algoritmo y aprender su funcionamiento. Utiliza los botones de la parte superior para controlar la evolución del algoritmo.