Cálculo del elemento mayoritario de un vector

Este problema parte de un vector \(v[1..n]\) de números naturales. Se quiere averiguar si existe un elemento que aparezca más de la mitad de las veces en el vector, es decir, \(2/n + 1\).

Para ello, el problema inicial se va dividiendo en subproblemas de la mitad de tamaño hasta llegar al caso trivial, que será aquel de tamaño 1, en el que el elemento mayoritario será él mismo. Posteriormente se combinan de nuevo los subproblemas, de forma que el algoritmo devolverá el elemento mayoritario de la combinación, o la indicación de que no existe. Por convención, se devolverá el valor -1 para indicar que no hay elemento mayoritario.

Como la función combinar recibirá los resultados de cada submitad, se pueden dar las siguientes situaciones:

• Si ambas partes devuelven -1, el resultado de la combinación será -1.
• Si una de ellas devuelve -1 y la otra no, indicará que la otra tiene elemento mayoritario y habrá que comprobar si es mayoritario de la combinación.
• Si ambas devuelven el mismo elemento mayoritario, ese elemento será el elemento mayoritario de la combinación.
• Si cada una devuelve un elemento mayoritario diferente, habrá que comprobar si alguno de ellos es elemento mayoritario de la combinación.

A continuación se muestra un ejemplo de su funcionamiento:

A continuación se muestra un ejemplo gráfico:

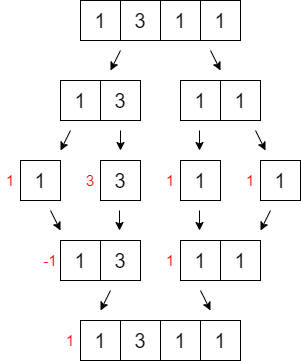
En el apartado de visualización podrás aprender su funcionamiento. Introduce los elementos del vector separados por comas y pulsa ACTUALIZAR. Podrás observar la evolución del algoritmo y las estructuras de datos mediante los botones de control de la parte superior.